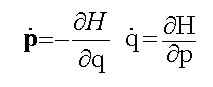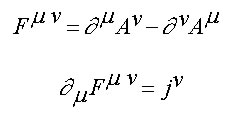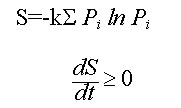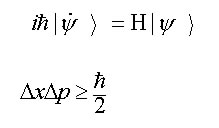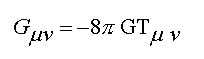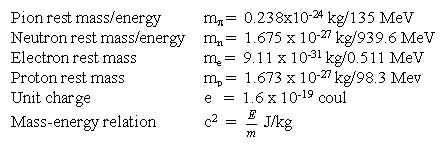El universo diseñado "justo a punto"

Introducción

¿Qué significa a nivel humano que un ingeniero diseñe un producto? En gran escala, ¿qué significaría decir que el universo es producto de un diseñador inteligente? ¿Y qué evidencia hay para apoyar esta afirmación? ¿Qué rasgos del universo sugieren que hay un "hogar" que ha sido elaborado cuidadosamente para nuestro beneficio? William Paley, en su obra clásica Natural Theology (1802), brindó evidencia tomada tanto de las ciencias físicas como de las biológicas a favor de un universo diseñado, pero la fortaleza de su argumento a favor del diseño estaba limitada por el conocimiento científico de su tiempo, y fue cuestionada posteriormente por la teoría de la evolución de Darwin. Sin embargo, los descubrimientos en astronomía y cosmología de la última mitad de siglo XX han provisto evidencia sumamente convincente a favor de un universo diseñado. Mi propósito en este artículo es brindar una indicación clara de lo que significa el diseño y luego resumir la base objetiva de la cosmología que indica que nuestro universo ciertamente está diseñado en forma única como un hábitat para la vida en general y para los humanos en particular.

¿Qué hace un ingeniero cuando diseña algo?

Para lograr entender lo que hacen los ingenieros cuando diseñan productos para los clientes, déjeme primero darle un ejemplo sencillo de cómo interactuamos con nuestro mundo cuando configuramos los sucesos físicos con un propósito. Suponga que quiero arrojar una bomba de agua desde la torre inclinada de Pisa a un amigo que está caminando en la plaza abajo (y no a otros turistas). Usando las ecuaciones que descubrió Newton para el movimiento y la atracción gravitatoria, yo podría describir el descenso de la bomba de agua hasta la plaza con la siguiente relación algebraica sencilla:

donde "G" es una constante universal que indica el valor de la fuerza de atracción gravitatoria, "m" y "r" son la masa y el radio de la tierra respectivamente, y "h₀" y "v₀" son la altura de la torre desde donde voy a arrojar la bomba y la velocidad vertical con la que la arrojo. Teniendo definidas estas constantes y estas condiciones iniciales, puedo entonces calcular la altura de la bomba de agua. H(t) da la altura calculada de la bomba de agua en función del tiempo "t" desde cuando la arrojé. Esta ecuación puede ser usada para garantizar que mi bomba llegará a la plaza en el momento justo como para pegarle a mi amigo. Todo lo que tengo que hacer es determinar en qué instante mi amigo paseante estará exactamente debajo de mí en la plaza, y entonces puedo usar la Ec. 1, para determinar la velocidad inicial con la que necesito arrojar la bomba. Simplemente dejar caer la bomba está bien también; basta poner v₀ = 0 y resolver para obtener el momento correcto para dejar caer la bomba. La precisión con la que debo especificar la velocidad de la bomba arrojada depende de la forma matemática de la Ec. 1, los valores especificados para la constante universal G y la condición inicial h₀. Con la simple forma matemática de la Ec. 1, la constante de la fuerza de gravedad G y la altura de la torre inclinada de Pisa, tendría que ser relativamente fácil pegarle a mi amigo.

Los tres factores que son esenciales para predecir el movimiento de la bomba de agua desde la torre inclinada hasta la plaza abajo ilustran los factores que generalmente son necesarios para brindar resultados determinados en el trabajo de ingeniería: (1) la forma matemática que asume la naturaleza (como se ilustra en la Ec.1); (2) los valores de las constantes universales (G en Ec. 1); y (3) las condiciones de borde, que incluyen la altura "h₀" de la torre desde donde arrojo la bomba y la velocidad inicial "v₀" con la cual arrojo la bomba. Los términos "m" y "r" pueden considerarse como las condiciones de borde adicionales que son propias de la ubicación de la torre sobre la superficie de la tierra (en vez de algún otro lugar del universo). El ingeniero no tiene ningún control sobre las leyes de la naturaleza y las formas matemáticas que asumen. Tampoco tiene control alguno el ingeniero sobre las constantes universales, como la constante de la fuerza de gravedad. El ingeniero sólo puede fijar las condiciones de borde, que se hace mediante dibujos de ingeniería que especifican exactamente cómo será el artefacto una vez fabricado.

Ilustremos este proceso de diseño con los requisitos (o condiciones de borde) que deben especificarse cuando un ingeniero diseña un automóvil. Debe determinar cuidadosamente las condiciones bajo las cuales la energía química en la gasolina será liberada y convertida en momento de torsión en las ruedas del auto. Cada dimensión de cada pieza del motor, por ejemplo, es crítica para que las piezas trabajen en conjunto en forma armoniosa. El tamaño absoluto y la forma de las piezas (a diferencia del tamaño relativo para que encajen unas con otras) depende de las fuerzas a ser desarrolladas y transmitidas, que a su vez dependen del peso del auto y la velocidad que alcanzará cuando esté funcionando. El peso depende del tamaño, que a su vez depende de la cantidad de pasajeros y equipaje que llevará el auto. Estos factores luego determinan el tamaño de los cilindros y los pistones a ser usados en el motor y la proporción de gasolina inyectada en estos cilindros. Los sistemas de frenos y de suspensión tienen que ser dimensionados independientemente para que coincidan con los requisitos de peso, así como las especificaciones de las cubiertas. Note cuántas especificaciones están relacionadas entre sí y, por lo tanto, no pueden ser asignadas independientemente. Cuanto mayor es esta interdependencia de las condiciones de borde, más complejos y exigentes son los requisitos de diseño. Pequeños errores en la especificación de cualquiera de estos requisitos producirán un auto con un desempeño muy inferior o, peor aún, un auto que no funciona para nada.

En las próximas secciones vamos a analizar si el universo tiene estas características esenciales que asociamos con el diseño. Los resultados determinados en el mundo natural dependen de (1) la forma matemática que asume la naturaleza; (2) los valores de las constantes universales; y (3) las condiciones iniciales, o condiciones de borde. Mientras los ingenieros sólo pueden fijar las condiciones de borde, la aptitud de universo como un hábitat para la vida en general y para los seres humanos en particular depende de las tres características. Por lo tanto, consideraremos cómo cada uno de estos requisitos aparece como esencial para la creación de un hábitat natural adecuado para la vida.

La asombrosa forma matemática que asume la naturaleza

La matemática es una actividad intelectual abstracta que comenzó en Grecia en el siglo VI a.C con Pitágoras y fue desarrollada por Euclides y Aristóteles. Sus estudios comenzaron con línea rectas y círculos y se extendieron a elipses, creadas por el seccionamiento de conos. En el siglo III a.C., Apolonias de Perga escribió ocho tomos monumentales dedicados a estas curvas, describiendo sus propiedades como "milagrosas." Sin embargo, nunca se les ocurrió a estos matemáticos que estas formas abstractas hermosas de la matemática eran en realidad descripciones de fenómenos del mundo real. Imagine el alborozo de Johannas Kepler (1571-1630) unos dieciocho siglos después, cuando descubrió que las órbitas de los planetas alrededor del sol se ajustaban a estas mismas formas matemáticas hermosas pero abstractas. Kepler señaló:

"El principal objetivo de todas las investigaciones del mundo exterior debería ser descubrir el orden racional y la armonía que le ha sido impuesto por Dios y que Él nos ha revelado en el lenguaje de la matemática."

Galileo Galilei (1564-1642) señaló que "las leyes de la naturaleza están escritas con la mano de Dios en el lenguaje de la matemática." Morris Kline, en su libro Mathematics: The Loss of Certainty (La matemática: la pérdida de la certeza - 1980) señala que los matemáticos religiosos del siglo XVI y XVII, incluyendo a Newton, Galileo, Kepler y Copérnico, creían que el universo era ordenado y, por lo tanto, estaba descrito por la matemática, porque un Dios racional lo construyó así. Kline dice que estos científicos/matemáticos creían que:

"Dios había diseñado el universo, y era de esperar que todos los fenómenos de la naturaleza siguieran un plan maestro. Una mente que diseñara un universo seguramente habría empleado un conjunto de principios básicos para regir todos los fenómenos relacionados."

Aun estos cristianos devotos se hubieran sorprendido indudablemente de saber que todos los fenómenos increíblemente variados que vemos en la naturaleza son el resultado de una cantidad tan pequeña de leyes físicas-cada una de las cuales asume una forma matemática sencilla-que pueden ser escritas todas en un lado de una hoja, como vemos en la Tabla 1.

Mecánica (ecuaciones de Hamilton)

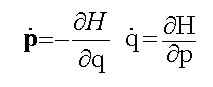
Electrodinámica (ecuaciones de Maxwell)

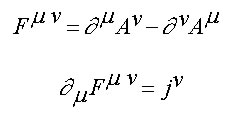
Mecánica estadística (ecuaciones de Boltzmann)

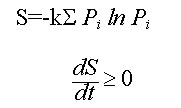
Mecánica cuántica (ecuaciones de Schrödinger)

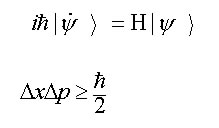
Relatividad general (ecuación de Einstein)

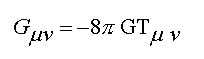
El físico Eugene Wigner, en un ensayo ampliamente citado titulado The Unreasonable Effectiveness of Mathematics in the Physical Sciences (La efectividad irrazonable de la matemática en las ciencias físicas - Comm. Pure and Appl. Math, 1960) señala que los científicos en general dan por sentado la efectividad notable y aun milagrosa de la matemática para describir el mundo real. En palabras de Wigner:

"La tremenda utilidad de la matemática es algo que bordea lo misterioso... No hay ninguna explicación racional para esto... El milagro de lo adecuado del lenguaje de la matemática para la formulación de las leyes de la física es un regalo asombroso que ni entendemos ni merecemos..."

Albert Einstein, en una carta a un amigo (1956, Lettres a Maurice Solovine), al comentar acerca de la comprensibilidad matemática del mundo, señaló:

"Tal vez le parezca extraño que yo considere la comprensibilidad del mundo al punto que podemos hablar de esta comprensibilidad como un milagro o un misterio eterno. Bueno, a priori uno debería esperar un mundo caótico, que no pueda ser comprendido de ninguna forma mediante el pensamiento... El tipo de orden creado, por ejemplo, por la teoría de la gravedad de Newton es de una especie bastante diferente. Si bien los axiomas de la teoría son postulados por un ser humano, el éxito de una empresa tal presupone un orden en el mundo objetivo de un alto grado, que a priori uno no tiene ningún derecho de esperar. Ese es el milagro que se vuelve cada vez más persuasivo con el desarrollo creciente del conocimiento."

A diferencia de Einstein y Wigner, pero de acuerdo con Newton y sus contemporáneos, muchos físicos modernos consideran que la forma matemática asombrosa que asume la naturaleza es una evidencia de un diseñador/creador inteligente-es decir Dios más que un misterio. Por ejemplo, el distinguido físico ruso, Alexander Polykov, señala que: "Sabemos que la naturaleza está descrita por la mejor matemática posible porque Dios la creó." El astrofísico australiano, Paul Davies, dice: "Las ecuaciones de la física tienen en ellas una simplicidad, una elegancia y una belleza increíbles. Eso en sí mismo es suficiente para probarme a mí que debe haber un Dios que es responsable de estas leyes y responsable del universo."

Pero la forma matemática por sí sola es insuficiente para garantizar un universo que sea un hábitat adecuado. La forma matemática particular también es crítica. Por ejemplo, es esencial que la forma matemática provea sistemas estables al nivel atómico o cósmico. Las soluciones de las ecuaciones de Hamilton para la mecánica no relativista newtoniana y para la teoría general de la relatividad de Einstein en la Tabla 1 para un sol con planetas sería inestable, a menos que la energía potencial gravitatoria sea proporcional a r^-1, un requisito que sólo se cumple para un universo con tres dimensiones espaciales. Para que la solución de la ecuación de Schrödinger (Tabla 1) para el átomo de hidrógeno dé niveles de energía estables y limitados, nuevamente se requiere un universo con tres (o menos) dimensiones espaciales. Las ecuaciones de Maxwell (Tabla 1) también sólo son válidas para un universo de tres dimensiones espaciales. Además, Courant y Hilbert (1962, Methods of Mathematical Physics - Métodos de la física matemática) han encontrado que la transmisión de señales electromagnéticas o acústicas de alta fidelidad están optimizadas en nuestro universo tridimensional, al decir:

"...este mundo nuestro, en el cual las señales acústicas o electromagnéticas son la base de la comunicación, parece haber sido escogido entre los modelos matemáticamente concebibles por su simplicidad y armonía."

En resumen, está claro que el carácter matemático específico de nuestro universo es esencial para que sea un hábitat adecuado para la vida; sin embargo, la razón por la que la naturaleza tiene esta forma matemática es problemática desde una metafísica naturalista.

El misterio de las constantes cosmológicas

Hay ciertas constantes universales que son una parte esencial de nuestra descripción matemática del universo. Encontramos una lista parcial en la Tabla 2, e incluye la contante de Planck (h), la velocidad de la luz (c), la constante de la fuerza de la gravedad (G), la masa del protón, del electrón, del neutrón, la carga unitaria del electrón o del protón, las constantes de la fuerza débil, de la fuerza nuclear fuerte y de acople electromagnético, y la constante de Boltzmann (k). Cuando se desarrollaron los modelos cosmológicos por primera vez a mediados del siglo XX, se suponía ingenuamente que la selección de un conjunto dado de constantes no era crítica para la formación de un hábitat adecuado para la vida. Los estudios posteriores de los parámetros que hicieron variar las constantes en forma sistemática han demostrado que cambios en cualquiera de las constantes produciría un universo dramáticamente diferente que no sería adecuado para la vida en ninguna forma imaginable.

Se han escrito mucho libros en los últimos diez años para detallar esta característica asombrosa de nuestro universo, a saber, que las constantes universales tienen que estar "justo a punto" para tener un universo apto para la vida. Una lista parcial incluye The Anthropic Cosmological Principle (El principio cosmológico antrópico) de Barrow y Tipler (1986), Universes (Universos) de John Leslie (1989), The Accidental Universe (El universo accidental) (1982), Superforce (Superfuerza) (1984) y The Cosmic Blueprint (El plano cósmico) (1988) de Davies, Cosmic Coincidences (Coincidencias cósmicas) de Gribbin y Rees, The Anthropic Principle (El principio antrópico) de Reinhard Breuer (1991), Universal Constants in Physics (Constantes universales de la física) de Gilles Cohen-Tannoudji (1993), The Creation Hypothesis (La hipótesis de la creación) editado por J.P. Moreland (1994) y Mere Creation (Mera creación) editado por William Dembski (1998). Voy a ilustrar este requisito de estar "justo a punto" para las diversas constantes universales y propiedades de la materia mediante varios ejemplos.

Constantes universales

Masa de las partículas elementales

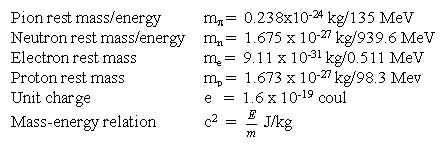
Constantes de la estructura fina

Constantes de la estructura fina-Cada una de las cuatro fuerzas de la naturaleza puede ser expresada adimensionalmente a fin de poder expresar sus fuerzas relativas según actúan en la naturaleza de una forma que facilite la comparación. Estas se resumen en la Tabla 2, y puede verse que varían en 10⁴¹, o 41 órdenes de magnitud (10 con 40 ceros adicionales después). Sin embargo, un cambio mínimo en cualquiera de estas constantes produce cambios dramáticos en el universo que lo convierten en inadecuado para la vida. Hay varios ejemplos que ilustran esta naturaleza de "ajuste fino" de nuestro universo.

Se ha encontrado que la magnitud relativa entre la fuerza de gravedad y la fuerza electromagnética es crucial por múltiples razones. Note en la Tabla 2 que la fuerza electromagnética es 10³⁸ veces mayor que la fuerza de la gravedad. Es la fuerza de gravedad la que junta a los protones en las estrellas haciendo que se fusionen entre sí con la consiguiente liberación de energía. La fuerza electromagnética hace que se rechacen. Debido a que la fuerza de gravedad es tan débil en comparación con la fuerza electromagnética, la velocidad a la cual las estrellas "arden" por fusión es muy lenta, lo que permite que las estrellas provean una fuente de energía estable durante un período muy largo. Si esta relación hubiera sido de 10³² en vez de 10³⁸ (es decir, la gravedad fuera mucho mayor), las estrellas serían mil millones de veces menos grandes, y arderían un millón de veces más rápido.

La distribución de frecuencia de la radiación electromagnética producida por el sol también es crítica, ya que necesita estar sintonizada con las energías de los enlaces químicos en la tierra. Si los fotones de la radiación fueran demasiado energéticos (demasiada radiación ultravioleta), entonces los enlaces químicos se destruirían y las moléculas serían inestables; si los fotones fueran demasiado débiles (demasiada radiación infrarroja), entonces las reacciones químicas serían demasiado lentas. La radiación producida depende de un equilibrio delicado entre la fuerza electromagnética (alfa-E) y la fuerza de gravedad (alfa-G), con la relación matemática que incluye (alfa-E)¹², lo que hace que la especificación de la fuerza electromagnética sea especialmente crítica. Por otro lado, la energía de enlace químico proviene de cálculos mecánicos cuánticos que incluyen la fuerza electromagnética, la masa del electrón y la constante de Planck. Por lo tanto, todas estas constantes tienen que ser dimensionadas en su relación mutua a fin de ofrecer un universo en el cual la radiación esté sintonizada con las reacciones químicas necesarias que son esenciales para la vida.

Otra coincidencia interesante de ajuste fino es que el espectro de emisión para el sol no sólo tiene un pico en un nivel de energía que es ideal para facilitar la reacción química sino que también tiene un pico en la ventana óptica para el agua. El agua es 10⁷ veces más opaco a la radiación ultravioleta e infrarroja que a la radiación en el espectro visible (lo que llamamos luz). Dado que el tejido vivo en general y los ojos en particular están compuestos mayormente por agua, la comunicación por la vista sería imposible si no fuera por el hecho que esta ventana única de la transmisión de la luz por el agua concuerda con la radiación del sol. Sin embargo, esta concordancia requiere una determinación cuidadosa de los valores de las constantes de la fuerza de gravedad y la fuerza electromagnética, además de la constante de Planck y la masa del electrón.

A continuación, considere el valor de la fuerza nuclear fuerte. El elemento más crítico de la naturaleza para el desarrollo de la vida es el carbono. Sin embargo, ha resultado aparente recientemente que la abundancia del carbono en la naturaleza es el resultado de un equilibrio muy preciso de la fuerza nuclear fuerte y la fuerza electromagnética, que determina los niveles de energía cuánticos de los núcleos. Sólo están permitidos ciertos niveles de energía para los núcleos y estos pueden considerarse como escalones de una escalera. Si la masa-energía de dos partículas que chocan da como resultado una masa-energía combinada que es igual o ligeramente menor que un nivel de energía permisible en la "escalera cuántica," entonces los dos núcleos se adherirán fácilmente o se fusionarán en la colisión, y la diferencia de energía necesaria para alcanzar el escalón será provista por la energía cinética de las partículas que chocan. Si este nivel de masa-energía para las partículas que se combinan es exactamente el correcto, o "justo a punto," entonces se dice que las colisiones tienen resonancia, lo cual significa una alta eficiencia de las colisiones que generan la fusión de la partículas que chocan. Si la masa-energía combinada da como resultado un valor que es ligeramente mayor que uno de los niveles de energía permisibles en la "escalera de energía," entonces las partículas simplemente rebotarán entre sí en vez de adherirse o fusionarse. Hoyle (1970) predijo la existencia del nivel de energía de resonancia desconocido del carbono, y posteriormente se encontró que existía. La fusión del helio y el berilio arroja un valor de masa-energía que es 4% menor que la energía de resonancia del carbono, que es compensado fácilmente por la energía cinética. De igual importancia fue el descubrimiento de que la masa-energía para la fusión del carbono con el helio era 1% mayor que el nivel de energía cuántico en la "escalera de energía" para el oxígeno, lo cual hace que esta reacción sea bastante desfavorable. Por lo tanto, casi todo el berilio se convierte en carbono, pero sólo una pequeña fracción del carbono es convertida inmediatamente a oxígeno. Estos dos resultados exigen la especificación del valor relativo de la fuerza nuclear fuerte y la fuerza electromagnética dentro de ~1%, lo cual es verdaderamente asombroso teniendo en cuenta su grandes valores absolutos y su diferencia en un factor de 100X, como vemos en la Tabla 2.

En forma más general, un aumento del 2% de la fuerza nuclear fuerte con relación a la fuerza electromagnética dejaría al universo sin hidrógeno, sin estrellas de larga duración que consumen hidrógeno y sin agua (que es una molécula compuesta por dos átomos de hidrógeno y un átomo de oxígeno), el solvente último para la vida. Una disminución de sólo 5% de la fuerza nuclear fuerte con relación a la fuerza electromagnética impediría la formación de deutones a partir de la combinación de protones y neutrones, lo que a su vez impediría la formación de todos los núcleos más pesados a través de la fusión de deutones para formar helio, la fusión del helio con el helio para formar berilio, y así sucesivamente. Rozental (1980) estima que la fuerza nuclear fuerte tuvo que ser entre 0,8 y 1,2 veces su valor actual para que hubiera deutones y todos los elementos de peso atómico 4 o superior.

Si la constante de acople de la fuerza débil (ver Tabla 2) fuera ligeramente mayor, los neutrones se descompondrían más rápidamente, reduciendo la producción de deutones y, por lo tanto, de helio y de elementos con núcleos más pesados. Por otra parte, si la constante de acople de la fuerza débil fuera ligeramente menor, el big bang habría consumido casi todo el hidrógeno convirtiéndolo en helio con el resultado final de un universo con poco o nada de hidrógeno y en cambio muchos elementos pesados. Esto no habría dejado ninguna estrella de larga duración y ningún elemento compuesto que contenga hidrógeno, especialmente agua. Breuer (1991) señala que la mezcla aproximada de hidrógeno y helio para proveer elementos compuestos que contengan hidrógeno, estrellas de larga duración y elementos más pesados es de aproximadamente 75% hidrógeno y 25% helio, que es justamente lo que encontramos en nuestro universo. Este equilibrio exige que la constante de acople de la fuerza débil (alfa-W) sea proporcional a la constante de acople de la fuerza de gravedad (alfa-G) en la siguiente proporción: (alfa-W)⁴ ~ (alfa-G), que podemos ver en la Tabla 2 que se cumple en la realidad.

Esta es sólo una lista ilustrativa pero no exhaustiva de ejemplos de coincidencias cósmicas que claramente demuestran que las cuatro fuerzas de la naturaleza han sido dimensionadas cuidadosamente para dar un universo que provee fuentes de energía de larga duración y una variedad de bloques constructivos atómicos que son necesarios para la vida. Se detallan muchos otros ejemplos en los libros citados, algunos de los cuales son bastante cómicos. Por ejemplo un valor más grande de la gravedad haría más probable que al caer nos quebremos debido a la fuerza de gravedad mucho mayor. Pero ¿qué deberíamos pensar acerca de partículas elementales y otras constantes universales como la velocidad de la luz y la constante de Planck? ¿Acaso también tiene que estar especificados muy precisamente?

Las masas de las partículas elementales y otras constantes universales-Ha sido sorprendente saber que las masas de las partículas elementales también deben ser especificadas muy cuidadosamente en su relación mutua y también con relación a las fuerzas de la naturaleza. Por ejemplo, Stephen Hawking (1980) ha señalado que la diferencia entre la masa del neutrón y la masa del protón debe ser aproximadamente dos veces la masa del electrón. La masa-energía del protón es de 938,28MeV, la masa-energía del electrón es de 0,51MeV, y el neutrón pesa 939,57 MeV. Si la masa-energía del protón más la masa-energía del electrón no fuera levemente menor que la masa-energía del neutrón, entonces los electrones se combinarían con los protones para formar neutrones, y toda la estructura atómica colapsaría, dejando un mundo de neutrones solamente. Si esta diferencia fuere mucho mayor, entonces todos los neutrones se descompondrían en protones y electrones, dejando un mundo de hidrógeno solamente, ya que los neutrones son necesarios para permitir que los protones se combinen para construir núcleos más pesados y los elementos asociados. Como están las cosas, el neutrón tiene justo el peso suficiente como para asegurar que el big bang haya generado un neutrón por cada siete protones, permitiendo una provisión abundante de hidrógeno como combustible para las estrellas y suficientes neutrones como para construir los elementos más pesados del universo. De nuevo, los valores relativos precisos para las masas de estas partículas elementales son considerados críticos para proveer un universo con fuentes de energía de larga duración y diversidad de elementos.

Brandon Carter (1970) ha provisto ejemplos de otras relaciones esenciales de las masas de partículas elementales a fin de permitir la formación de elementos más pesados en la naturaleza: la fuerza fuerte debe estar relacionada con la masa del neutrón y la masa del pión por (alfa-S)² ~ 2 (masa del neutrón/masa del pión); la constante de la estructura fina electromagnética (alfa-E) ~ [(masa del neutrón) - (masa del protón)] / (masa del pión); y la estructura fina de la fuerza nuclear fuerte debe obedecer (alfa-S)² ~ 1 / (9 alfa-E). La Tabla 2 puede ser usada para mostrar que cada uno de estos requisitos se cumple en la realidad. Es notable que se satisfagan todos estos requisitos, a pesar del hecho que estas masas y fuerzas parecen ser independientes en su asignación y no están conectados causalmente. Podrían afirmarse también requisitos adicionales para h, k, c y otras constantes.

Concluiremos esta sección sobre las coincidencias cosmológicas permitiendo que varios científicos distinguidos den su opinión acerca de las observaciones reseñadas más arriba. Por ejemplo, Freeman J. Dyson dice:

"Cuando miramos afuera hacia el universo e identificamos los muchos accidentes de la física y la astronomía que han resultado en nuestro beneficio, casi parece como si el universo debe haber sabido en alguna forma que estábamos llegando nosotros."

El ganador del premio Nobel, Arno Penzias, hace esta observación acerca del carácter enigmático del universo:

"La astronomía nos lleva a este evento único, un universo que fue creado de la nada y que está equilibrado delicadamente para proveer exactamente las condiciones requeridas para sustentar la vida. En la ausencia de un accidente absurdamente improbable, las observaciones de la ciencia moderna parecen sugerir un plan subyacente que podríamos llamar sobrenatural."

Sir Fred Hoyle, el famoso astrónomo británico que al principio (1951) argumentaba que las coincidencias eran sólo eso, coincidencias, para 1984 había cambiado de opinión, según se desprende de esta cita:

"Estas propiedades parecer atravesar la trama del mundo natural como una hebra de felices coincidencias. Pero hay tantas coincidencias extrañas esenciales para la vida que parecen exigir alguna explicación para justificarlas."

Los requisitos asombrosos para las condiciones iniciales

La forma matemática específica que asume la naturaleza y los valores altamente específicos de las diversas constantes universales y las masas de las partículas elementales no puede explicar por sí solos nuestro hábitat y la vida. Todo esto podría haber sido hecho de forma elegante, como ocurrió y explicamos arriba, y aun así la vida no hubiera ocurrido si las condiciones de borde en ciertos puntos críticos no hubieran sido fijados adecuadamente. En esta sección, discutiremos las condiciones iniciales para el big bang. Existe un problema similar para el origen de la vida y para la explosión del Cámbrico, pero dejaremos la discusión de estos temas para artículos más detallados en otra parte de esta edición especial.

El problema de valores de borde (o condiciones iniciales) fundamental con el big bang es el carácter crítico de la velocidad inicial. Si esta velocidad hubiera sido demasiado grande, la materia en el universo se habría expandido demasiado rápidamente y nunca se habrían formando los planetas, las estrellas y las galaxias. Si la velocidad inicial hubiera sido demasiado baja, el universo se habría expandido sólo por un tiempo breve y luego habría colapsado rápidamente bajo la influencia de la gravedad. Los modelos cosmológicos bien aceptados nos dicen que la velocidad inicial debe estar especificada con una precisión de 1 / 10⁵⁵. Este requisito parece superar largamente a la casualidad y ha sido el impulso para alternativas creativas, más recientemente el modelo inflacionario del big bang. Sin embargo, la inflación misma parece exigir un ajuste fino para que ocurra y para que arroje irregularidades ni demasiado pequeñas ni demasiado grandes para que se formen las galaxias. Inicialmente, se estimaba que dos componentes de una constante cosmológica impulsora de la expansión debían cancelarse entre sí con una precisión mejor que 1 parte en 10⁵⁰. Más recientemente, en Scientific American (enero de 1999), se afirma que la precisión requerida es de 1 parte en 10¹²³. Además, la relación entre la energía gravitatoria y la energía cinética debe ser igual a 1,000000 con una variación de 1 parte en 100.000. Esta es un área de investigación activa en este momento y estos valores podrían cambiar con el tiempo. Sin embargo, parece que los requisitos esenciales de las condiciones de borde altamente especificadas estarán presentes para cualquier modelo que sea confirmado finalmente para el origen de big bang del universo.

Resumen

Mi ejemplo inicial de diseño era uno muy sencillo que involucraba una sola ley física, una constante universal y dos condiciones iniciales que podían ser determinadas de forma tal que mi bomba de agua llegara sobre la plaza de la torre inclinada de Pisa en el momento justo como para pegar a mi amigo paseante. Este es un problema de diseño relativamente sencillo. Sin embargo, para que el universo tuviera estrellas que generaran una diversidad de elementos, que proveyeran fuentes de energía a largo plazo con una radiación de longitud de onda adecuada para facilitar las reacciones químicas, y satisfacer muchos otros requisitos de un hábitat adecuado para la vida y para el origen de la vida, la forma matemática de las leyes de la naturaleza, las 19 constantes universales (no todas listadas en la Tabla 2), y muchas condiciones iniciales deben estar "JUSTO A PUNTO." Muchos de estos requisitos están interrelacionados. Por ejemplo, el requisito de la velocidad inicial está relacionado con el valor de la fuerza de gravedad. Hay tantos requisitos distintos interrelacionados que parece difícil imaginar cómo todos estos resultaron "accidentalmente" como necesitaban ser. Debido a los muchos requisitos cruzados, parece improbable que haya un conjunto alternativo de valores para estas constantes que "funcione." Además, los valores necesarios abarcan treinta órdenes de magnitud (10³⁰), lo cual hace que su "selección" correcta accidental sea mucho más notable. Es bastante fácil comprender por qué tantos científicos han cambiado de opinión en los últimos 30 años, y están de acuerdo en que se requiere una gran dosis de fe para creer que el universo puede ser explicado como nada más que un accidente cósmico fortuito. La evidencia a favor de un diseñador inteligente se vuelve más convincente cuanto más comprendemos acerca de nuestro hábitat cuidadosamente fabricado.

Traducción: Alejandro Field